函数概念优质课教案.docx

函数概念优质课教案.docx

《函数概念优质课教案.docx》由会员分享，可在线阅读，更多相关《函数概念优质课教案.docx（11页珍藏版）》请在冰点文库上搜索。

函数概念优质课教案

福清洪宽中学观摩课（优质课）教案

教师

施信飞

学科

数学，

班级

福清二中

初二

（2）班

课题

19.1.1函数的概念

时间

2015年4月24日

教学目标

1了解函数的概念，自变量取值围概念；2正确判断是否是函数关系，掌握确定自变量取值围的方法，并在实际问题中那个确定函数关系式并加以应用；3提高分析解决问题能力，知识应用能力，解不等式组的能力等等

教学重点

确定函数关系式并应用计算以及确定自变量的取值围

教学难点

结合实际问题意义确定自变量的取值围

教学步骤

（体现教学容、教学问题设计、时间安排、板书设计、学法指导、作业布置和预习等）

教学方法

教学手段

一．复习引入：

①小明到商店买练习簿，每本单价2元，购买的总数x（本）与总金额y（元）的关系式，可以表示为_____________；

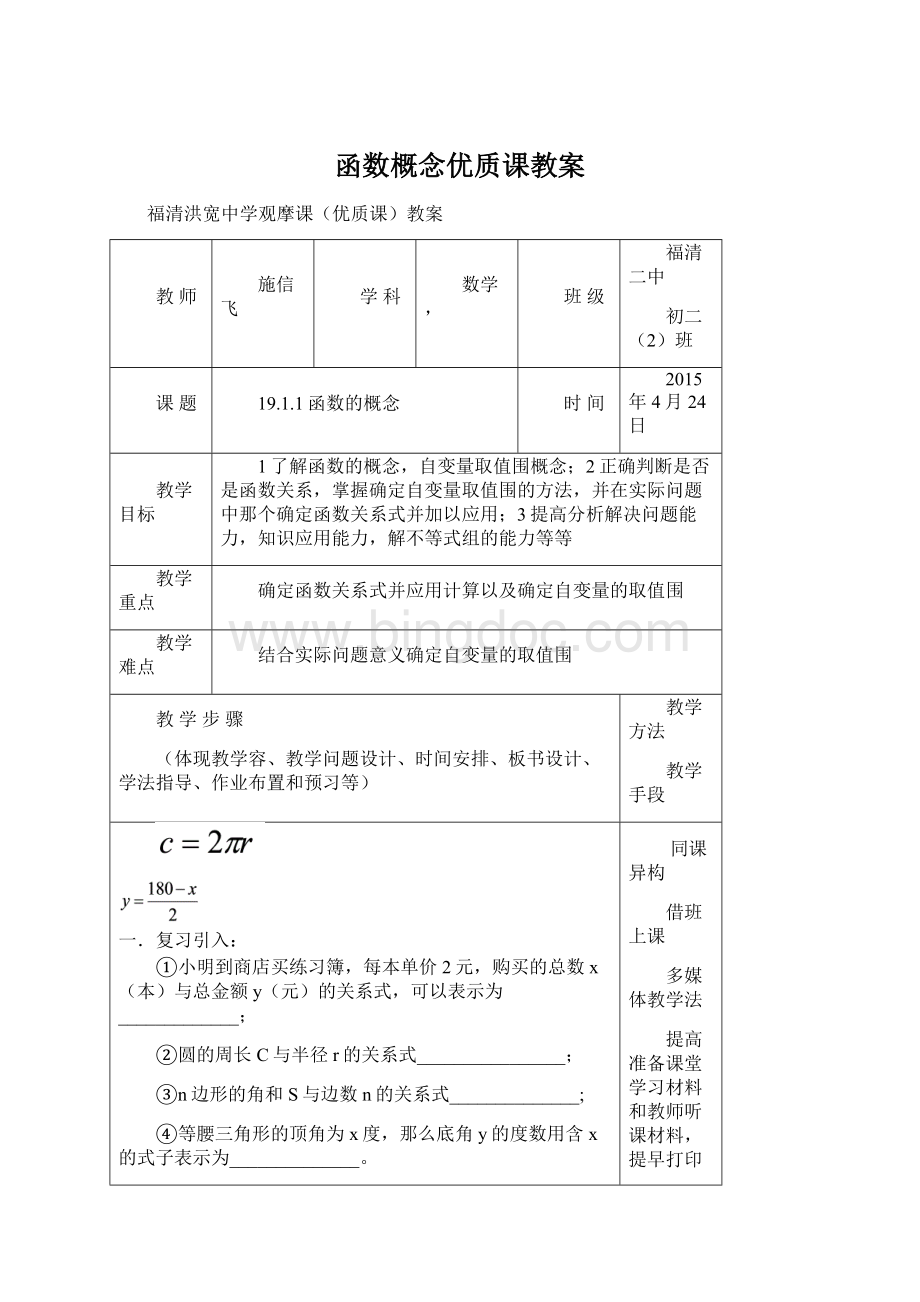
②圆的周长C与半径r的关系式________________；

③n边形的角和S与边数n的关系式______________;

④等腰三角形的顶角为x度，那么底角y的度数用含x的式子表示为______________。

分析：

①总价=单价×数量，即：

y=2x②圆周长

③多边形角和公式S=（n-2）×1800

④由三角形角和定理及等腰三角形的性质可得：

顶角+2×低角=1800即：

x+2y=1800化简得：

二．新课讲解：

同课异构

借班上课

多媒体教学法

提高准备课堂学习材料和教师听课材料，提早打印并分发给学生。

教学步骤

教学方法

教学手段

请同学们根据题意填写下表:

1y=2x

x（本）

1

2

3

4

5

y（元）

2

半径r

1

2

3

4

5

圆周长C

③S=（n-2）×1800

边数n

3

4

5

6

…

角和S

3

顶角x

300

400

500

600

…

底角y

分析：

按照关系式，根据表格中已知的一个变量的值代人关系式中计算，求出另个变量的值，你计算对了吗？

观察以上的四个式子，你发现它们有什么共同点？

通过①到④复习常变量的概念，同时引入函数的概念，引导学生观察题中所含的是两个变量；

通过填写表格，让学生理解函数的概念中的一一对应关系。

当一个变量有一个值时，另一个变量有几个值与之对应？

教学步骤

教学方法

教学手段

一般地，在一个变化过程中，如果有两个变量，（假定为x和y），对于x的每一个确实的值，y都有唯一确定的值与其对应，那么我们就说x是自变量,y是因变量,y是x的函数。

其中我们可以发现满足是函数关系的三个特点：

（1）两个变量；

（2）两个变量之间有对应关系；（3）取定x的每一个值，y都有唯一的值与x对应。

即：

函数是表示两个变量之间一一对应关系。

例1判断下列问题中的变量y是不是x的函数?

（1）在y=2x中的y与x；

（2）在y=x2中的y与x；

（3）在y2=x中的y与x；

分析：

结合函数的定义，判断是否满足函数的三个前提条件，

即两个变量之间的一一对应关系。

其中题（3）中当x=1时

即y2=1,此时y的值是多少？

是唯一值吗？

三．课堂练习：

①判断下列问题中的变量y是不是x的函数?

（1）在

中的y与x；

（2）在y=│x│中的y与x；

（3）在│y│=x中的y与x；

②下列变量之间的关系中，具有函数关系的有（）

（1）三角形的面积与底边；

（2）多边形的所有对角

了解函数概念，

了解对应关系，了解一一对应关系。

通过例题1巩固函数的概念，促进学生进一步理解函数的概念

注意函数的概念与函数是否有意义的不同点。

两者不能混淆理解。

教学步骤

教学方法

教学手段

线条数与边数；（3）圆的面积与半径；（4）y=

中的y与x。

A.1个B.2个C.3个D.4个

分析：

题①

中函数关系与函数是否有意义是两个概念

后两小题和例题1中后两小题相类似；题②中

（1）含有三个变量其他都是函数关系。

思考题：

课本P73

（2）

在下面的我国人口统计表中，年份与人口数可以记作两个变量x与y，对于表中每一个确定的年份（x），都对应着一个确定的人口数（y）吗？

年份

人口数（亿）

1984

10.34

1989

11.06

1994

11.76

1999

12.52

此时，y是x的函数吗？

思考题：

课本P73

（1）

如图，是体检时的心电图，其中横坐标x表示时间，纵坐标y表示心脏某部位的生物电流，它们是两个变量，其中y是

x的函数吗？

实际问题中的函数的判断：

2是否满足两个变量；

②是否形成一一对应关系。

了解函数的其他表示方式，只要满足函数的概念，就可以确定是否是函数关系。

教学步骤

教学方法

教学手段

分析：

只要满足函数定义，就可以判断是否是函数关系。

练习：

下列各曲线中不表示y是x的函数的是（）

分析：

在坐标系中寻找x的一个值，寻找相对应的y的值有几个？

若只有一个点那么y就是x的函数；如果不只有一个点，那么y就不是x的函数。

对于函数y=2x,取定x=3,y都有唯一的值6与x=3对应，

此时我们把6叫做当自变量的值为3时的函数值

数形结合法

从图像上理解函数的概念，就是在坐标系中。

对于一个横坐标x的值，有没有两个或以上的纵坐标y的值与x对应？

如果有两个以上的点，那么图像就不是表示函数关系。

教学步骤

教学方法

教学手段

一般地，如果当x=a时,y=b,则b叫做当自变量为a时的函数值。

例2，已知函数y=（x+1）2

（1）若x=1，求y的值

（2）若y=1求相应的x的值

分析：

题

（1）把x的值代人函数关系式中计算，求出相应的y的值；题

（2）把y的值代人函数关系式中计算，求出相应的x的值。

注意平方和开平方运算。

能够满足函数关系式有意义的所有自变量的值叫做自变量的取值围。

例3求出下列函数中自变量的取值围

（1）y=2x

（2）

（3）

（4）

分析：

若解析式是整式，自变量取全体实数；如

（1）

若含有分式，满足分母不等于0，列出不等式，解出自变量的取值围。

如（3）；若含有二次根式，满足被开方式不小于0，列出不等式求解。

如

（2）。

题（4）包含分式和二次根式，联立不等式组求解。

函数的应用：

1求值

已知x求y;已知y求x.

②确定自变量取值围。

结合分式和二次根式的定义和性质，必要时两者都要考虑，组成不等式组求解。

教学步骤

教学方法

教学手段

例4一辆汽车的油箱中现有汽油50L，如果不再加油，那么油箱中的余油量y（单位：

L）随行驶里程x（单位：

km）的增加而减少，平均耗油量为0.1L/km。

（1）写出表示y与x的函数关系的式子。

（2）指出自变量x的取值围

（3）汽车行驶200km时，油箱中还有多少油？

分析：

题

（1）根据；耗油量+剩余的油量=总油量50

L；耗油量=平均耗油量0.1×行驶里程，即0.1x+y=50，

从而y=50-0.1x;题

（2）中同时满足x≥0.y≥0即：

x≥0

及50－0.1x≥0解得0≤x≤500；（3）中已知的是哪个

值等于200，（x=200）然后再代人函数关系式进行计

算。

最后分别进行作答。

课堂练习：

实际问题中的函数关系式的确定要结合实际问题中的量之间的关系，再转化为函数关系式。

在确定自变量取值围时要注意实际问题的实际意义。

教学步骤

教学方法

教学手段

3.等腰三角形ABC的周长为10,底边BC长为y,

腰AB长为x,求:

（1）y关于x的函数解析式;

（2）腰长AB=3时,底边的长;

（3）自变量的取值围。

分析：

（3）中考虑x﹥0,y﹥0,2x﹥y组成不等式组求解。

4.在函数

中，自变量

的取值围是（　　）

Ａ．

且

Ｂ．

且

Ｃ．

Ｄ．

5.在函数

中，自变量

的取值围是

6.在计算器上按下列程序进行操作：

填表：

讲练结合法，教师在学生做练习期间进行巡视，对于个别学生出现的缺漏给予当面辅导，有的放矢。

教学步骤

教学方法

教学手段

7.打开某洗衣机开关（洗衣机无水），在洗涤衣服时，洗衣机经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量

（升）

与时间

（分钟）之间满足某种函数关系，其函数图象大致为（）

8.我市大部分地区今年5月中、下旬的天气情况是

前5天小雨，后5天暴雨．那么能反映我市主要河流

水位变化情况的图象大致是（　　）

对于完成较好的学生给予表扬，多多肯定，提高学生学习的信心。

教学步骤

教学方法

教学手段

四，课堂小结：

1.函数定义：

（三要素）两个变量一一对应关系

2.函数关系式应用：

（1）求值：

①已知x求y②已知y求x；

（2）确定自变量取值围（注意自变量本身的意义还要考虑在实际问题中的实际意义）

（3）实际问题中函数关系式的确定，注意审题，列出关系式再进行转化成函数关系式。

五．板书设计：

函数

函数值

自变量取值围

六．课后作业：

课本P812;3;4;5

预习：

函数的图像

与学生进行归纳本节课学习容，看看自己这节课掌握了多少？

在轻松，愉快的气氛中结束这节课。

教后随笔